问题描述:
详细推理下面的公式

✅ 推导过程:
原始公式
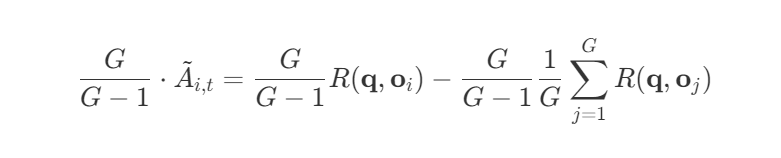
第一步:展开 $\tilde{A}_{i,t}$
假设
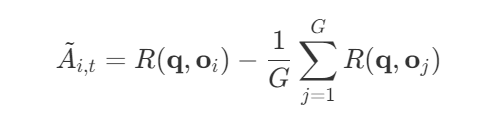
即 $\tilde{A}_{i,t}$ 是当前样本的reward减去所有样本reward的平均。
第二步:将 $\tilde{A}_{i,t}$ 带入
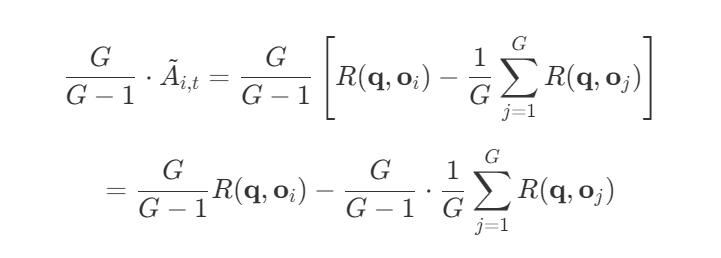
第三步:化简第二项
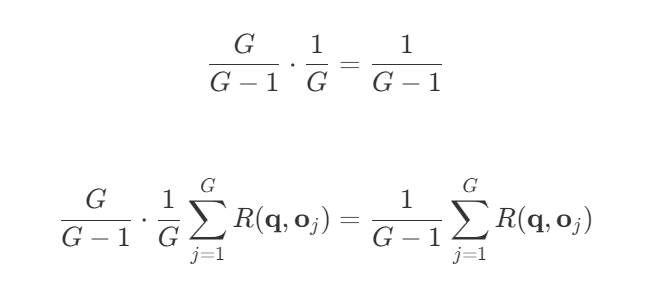
第四步:合并
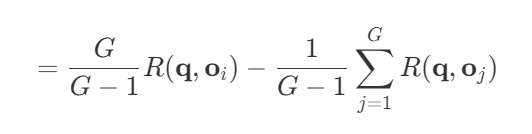
第五步:将 $\sum_{j=1}^G$ 拆开
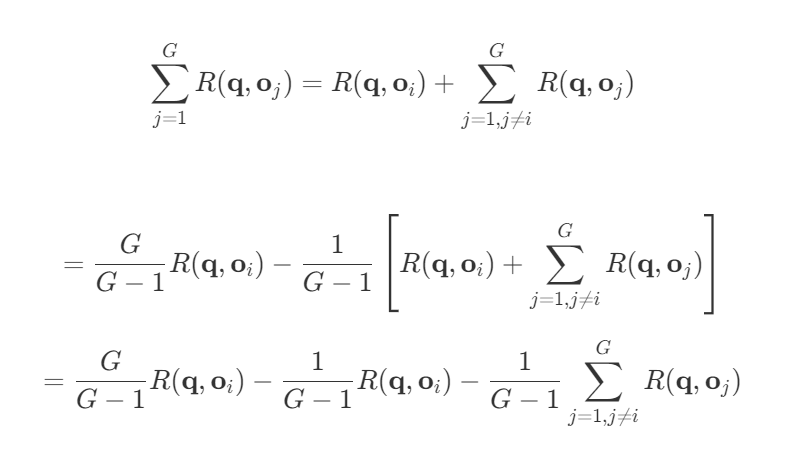
第六步:合并 $R(\mathbf{q}, \mathbf{o}_i)$ 的系数
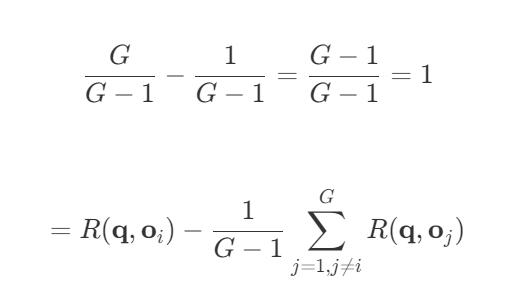
第七步:写成常见的 leave-one-out (RLOO)形式

总结
公式推导的详细步骤如下:
- 展开 $\tilde{A}_{i,t}$ 的定义。
- 用分数系数 $\frac{G}{G-1}$ 乘进去,并拆分项。
- 合并系数,化为 $R(\mathbf{q}, \mathbf{o}_i)$ 和除去 $i$ 的其余项的平均。
- 得到 leave-one-out 形式的 advantage。
简要总结:
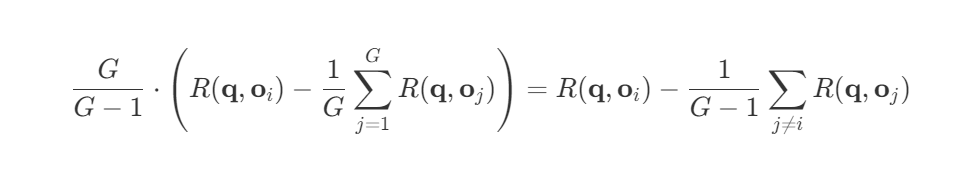
结语
第三百三十八篇博文写完,开心!!!!
今天,也是充满希望的一天。



